绝对值特点：灵活，综合性比较强，可综合函数，方程，不等式，图像等等进行考察。
关键：去绝对值
方法：定义法，零点分段讨论法，几何意义法。
绝对值考点梳理：绝对值定义，绝对值几何意义考察，绝对值自比式，绝对值非负性，等价性等相关性质考察，绝对值基本不等式及绝对值三角不等式求解最值和证明，绝对值方程，不等式求解，绝对值方程解的个数问题，绝对值函数图像与其最值问题。
1.绝对值定义：
已知绝对值内部表达式的符号，可以通过定义法进行去绝对值，多用于绝对值方程，绝对值不等式，最为简单有效摆脱绝对值的束缚。
2.绝对值几何意义考察：
将所求式子建立和图像之间的联系，更快得到函数图像，以及方程的解，尤其针对于当一个未知数的有多个绝对值，且绝对值里面未知数系数相同的时候，比零点分段讨论更为高效进行求解。
3.绝对值自比式：
题眼：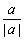
解题思路：将每一个式子进行正负性讨论，关键判断有几正几负。
4.绝对值性质：
题干当中出现绝对值，根号，平方项等多个非负性的式子注意可能考察非负定零。
出现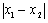
等式子的时候注意可能需要利用等价性进行转化，构造与韦达定理的相关两个式子。
5. 绝对值三角不等式：
绝对值三角不等式一般是用于求带有绝对值的最值或者证明带有绝对值不等式相关题型。三种常考题型：
（1）取等：发现和或差的整体部分，利用取等条件得到不等式，再对不等式进行求解；或者利用已知取等条件的不等式，得到取等部分，进而求解。
（2）求最值：使未知数前的系数是相反数，构造出定值，即为最值。
（3）证明：利用整体的部分的关系进行双向证明。
题眼：|a|，|b|，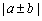
。
解题步骤：对原式重组，以期利用条件；带入公式进行化简、求解。
6.绝对值方程与不等式求解：
利用定义法、平方法、分段讨论法或几何意义整理原式，使等号一边含有绝对值，另一边不含绝对值，但是一定要注意两边式子都是具有非负性，注意验根；直接利用定义法去掉绝对值符号，分别求解，使不等号一边含有绝对值，另一边不含绝对值；利用“大于号取两端，小于号取中间”去掉绝对值符号，分别求解。
7.绝对值方程与不等式求解：
利用定义法、平方法、分段讨论法或几何意义整理原式，使等号一边含有绝对值，另一边不含绝对值，但是一定要注意两边式子都是具有非负性，注意验根；直接利用定义法去掉绝对值符号，分别求解，使不等号一边含有绝对值，另一边不含绝对值；利用“大于号取两端，小于号取中间”去掉绝对值符号，分别求解。
8. 绝对值方程解的个数问题：
核心：利用绝对值与函数图像交点判断，注意图像的翻转和最值。
绝对值这个部比分虽然是较基础、比较简单、比较容易理解的一部分内容，涉及的知识点有些庞杂，所以需要同学们在复习过程中一定要分好类别，要有耐心、要细心、要认真地去复习，并且要结合相应的题对自己的学习效果进行相应的考查，以查漏补缺。
